SSH стал основным способом работы с удаленными машинами как на Linux, так и windows. Тем острее встал вопрос о необходимости доступа к файлам на удаленной машине.
Тем у кого есть облачные сервисы от keenetic, можно не читать, там всё сделано грамотно и доходчиво, достаточно только настроить и пользоваться.
Мне же удовольствие keenetic недоступно финансово, поэтому я реализую более простое решение.
SSHFS это виртуальная файловая система, которая позволяет представить любой ssh-ресурс в качестве папки в Linux или сетевого диска в Windows.
Для организации такого диска лучше использовать специальную утилиту, позволяющую удобно настроить и в один клик подключать сетевые диски по протоколу ssh.
Чтобы скачать эту утилиту, нужно перейти по ссылке https://github.com/evsar3/sshfs-win-manager
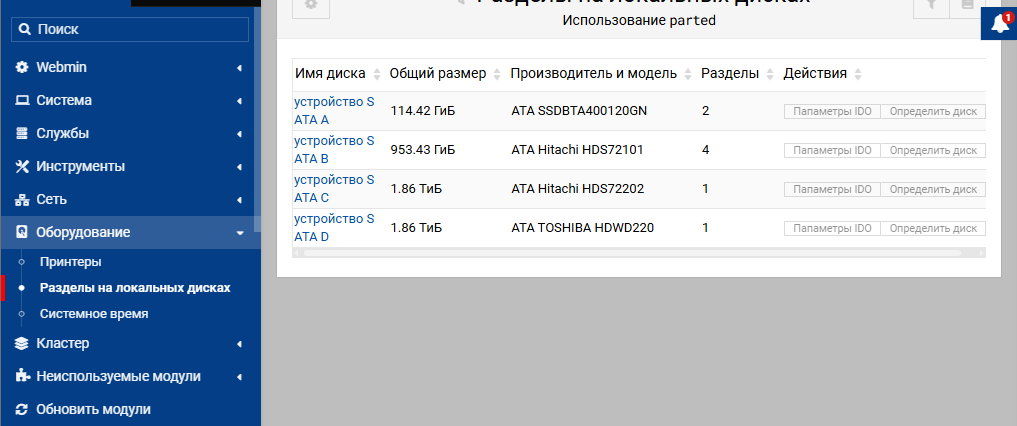
После установки достаточно настроить ресурсы, которые потом будут подключаться и выглядеть, как локальные диски.
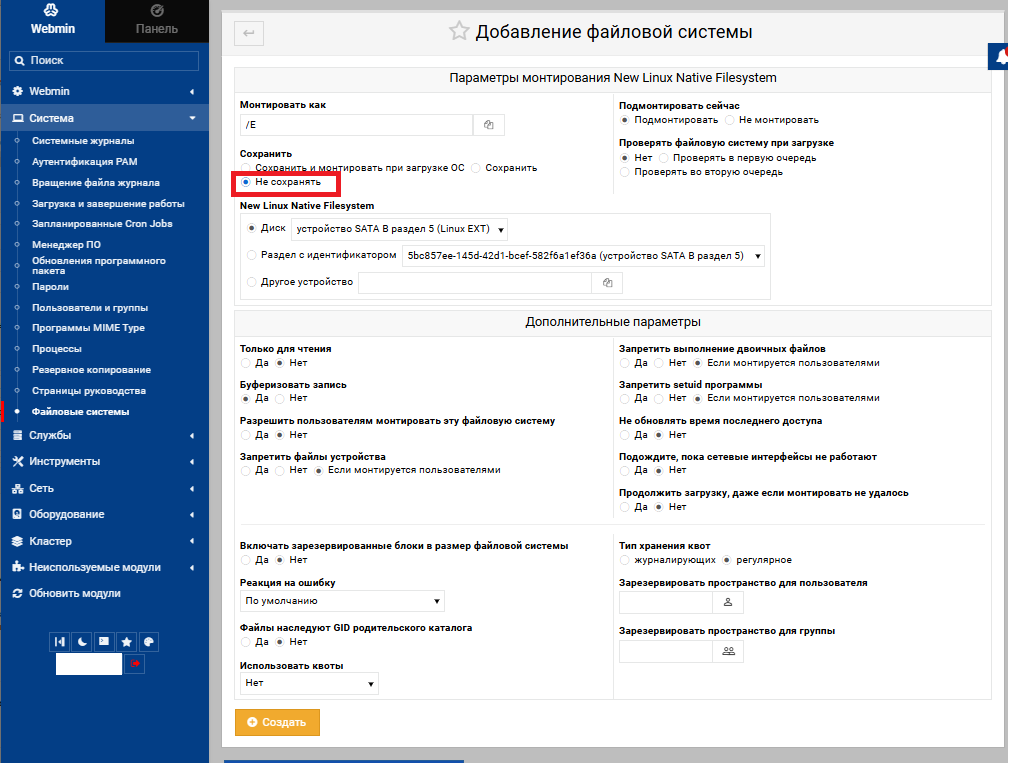
Вид настроенной утилиты показан на картинке ниже
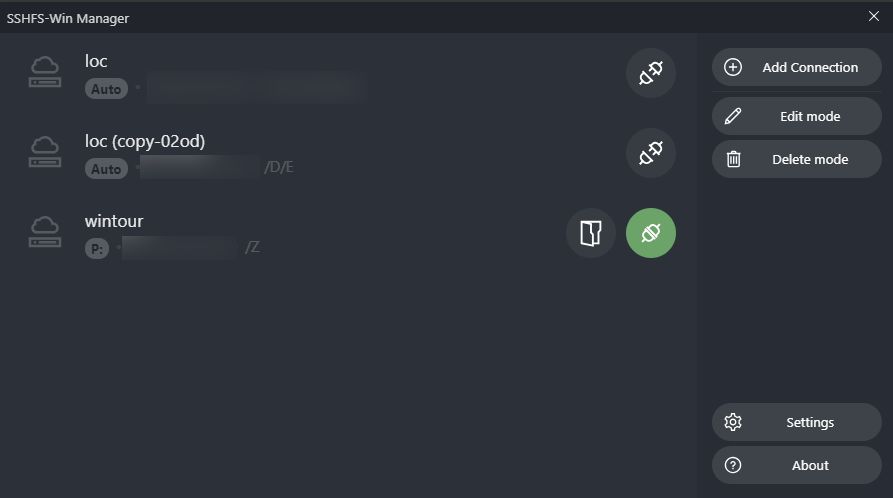
Чтобы добавить ваш ресурс, необходимо нажать кнопку «add connection».
Откроется окно настройки подключения:
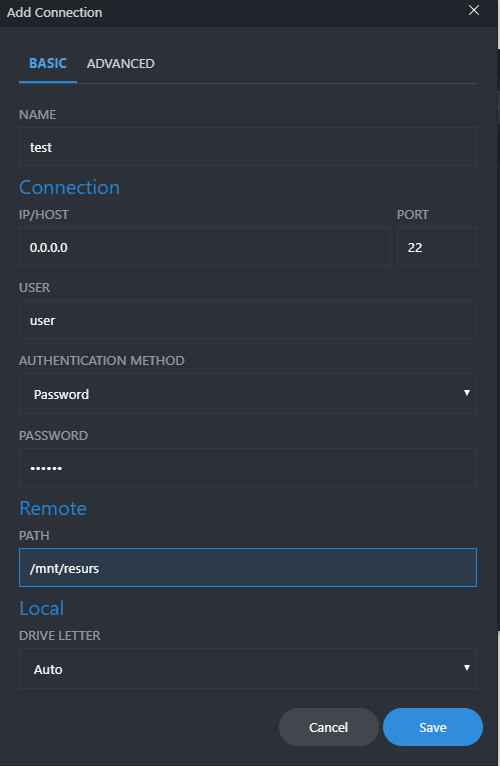
Здесь в поле NAME необходимо указать имя ресурса, так он будет отображаться в системе Windows/
В поле IP/HOST требуется указать ip-адрес машины, либо доменное имя удаленного ПК. Если подключение выполняется по локальной сети и настроен локальный DNS, то сетевое имя будет host.local или host.yourdomain.local. host это имя машины.
В поле PORT необходимо указать «порт» на котором «слушает» удаленный ssh. Если удаленный компьютер находится за NAT (роутер, шлюз), то на роутере необходимо выполнить «проброс» портов. В локальной домашней сети ничего делать не нужно.
В поле USER необходимо ввести имя пользователя.
Поле AUTHENTICATION METHOD предлагает один из трёх способов авторизации на удаленной машине. Пароль, пароль, сохраняемый в программе, пароль, спрашиваемый при каждом подключении, или по открытому ключу. Какой способ авторизации использовать, выбирать читателю.
В поле PATH должен быть указан полный путь к папке на удаленном ресурсе. У каждого пользователя он будет свой, если удаленная машина разрешает, то можно подключиться и к корневому каталогу «/»
Поле DRIVE LETTER снабжено выпадающем списком и предлагает назначить любую не занятую букву как локальному диску.
После ввода данных требуется сохранить параметры.
Данное окно закроется и останется главное окно программы:
…в котором необходимо нажать на кнопку «подключить» (смотри картинку выше).
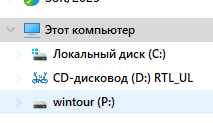
Если всё нормально, то ресурс будет подключен, а в проводнике отобразится новый диск, как локальный:
В Linux ничего устанавливать обычно не требуется, любой ресурс SSH подключается из файлового менеджера методом «подключиться к серверу», система всё сделает самостоятельно.
Плюсы такого способа:
- Отсутствуют системные ограничения на размер файла. Это значит, что вы можете делать бэкапы по зашифрованному каналу без ограничений на размер файла.
- Подключенный ресурс работает как локальный диск и его можно использовать напрямую.
- Нет прослоек в виде веб-серверов типа Apache2 или IIS.
- Не требуется SSL сертификат, соединение зашифровано.
- Одинаково хорошо работает как в Windows, так и в Linux.
Минусы:
- Возможные ограничения на работу протокола SSH провайдером, если вы работаете с удаленным ресурсом через Интернет. В этом случае требуются меры для маскировки трафика под https.
- Возможно снижение скорости обмена данными на узких каналах из-за шифрования.
- SSH хоть и хорошая вещь, но не панацея, существуют известные уязвимости серверной части, поэтому при работе через Интернет необходимы индивидуальные средства защиты от вторжений.
- Требуется достаточно глубокое знание и грамотная организация сети.
А почему не WebDav?
Есть несколько причин, по которым я вижу Webdav плохим решением для организации облачного или сетевого хранилища.
Оставим в стороне факт, что webdav разработан корпорацией Microsoft и его реализация за пределами Windows и коммерческих решений выглядит не лучшим образом. Но причины выглядят следующим образом:
- Сложность настройки сервера. Для того, чтобы настроить сервер на работу с WebDav требуется использовать IIS на Windows и любой web-сервер на Linux-системах. Требуется доменное имя и SSL-сертификат. На 2025 год у нас практически не осталось клиентов, которые бы не требовали TLS-шифрования http — трафика. И подключиться к webdav-ресурсу без шифрования в 2025 году будет проблемой.
- Встроенные ограничения на размер файла в операционных системах. В Linux на трафик по протоколу WebDav действует ограничение в 2 Гб на один файл. Причем я не смог выяснить можно ли снять это ограничение. Но раз keenetic — производитель сетевого оборудования смогли снять это ограничение, значит способы есть и они закрыты коммерческими лицензиями, и именно поэтому нет вразумительных ответов на запросы, связанные с ограничением. А такие решения, как Nextcloud вносят больше проблем при работе по WebDav, чем пользы.
В Windows ограничения изменяются разными методами. Полностью не снимаются, но их можно отодвинуть.
Что я такого большого перекачиваю в одном файле? Не ваше дело. - Сложность с доступом к ресурсу по WebDav с разных устройств. Я на себе испытал эту проблему. Проводник Windows, любые файловые менеджеры Linux и Андроид по-разному ведут себя с одним и тем же webdav ресурсом. И нет единого способа подключиться к одному ресурсу. Поэтому на данный момент webdav мной практически не используется.
Вместо вывода.
Существующие протоколы доступа к файлам через сеть имеют и недостатки, и достоинства. В одном случае необходимо минимум настроек и времени на организацию, но зато протокол имеет единый стандарт и работает с удаленной системой на уровне этой самой систем. В другом случае мы имеем костыль в виде надстройки над надстройкой, чтобы организовать какой-то способ хранения данных. По мне он выглядит малонадежным и слишком сложным для организации хранилища, отвечающего единому стандарту хранения и обмена данными. Однако, благодаря TLS шифрованию он может применяться как способ организации виртуальных хранилищ данных, таких как известные облачные сервисы.
Что применять, выбирать Вам.